| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- nodejs 기초
- c언어 스코프
- c언어 라이프타임
- C++
- 통근버스 출발 순서 검증하기
- c언어 지역변수
- softeer
- GStreamer tutorial
- 코딩테스트 기출
- Sparkfun Edge Example
- Spakrfun Edge
- c언어 전역변수
- c언어 정적변수
- 플레이페어 암호
- c언어 static
- 사물인식 최소 면적 산출 프로그램
- GStreamer
- 수퍼컴퓨터 클러스터
- GStreamer 튜토리얼
- MacOS 설치
- Sparkfun Edge 프로젝트
- 삼성 B형
- 소프티어
- SKT FLYAI
- C++해설
- 코테기출
- 삼성전자 #영상디스플레이사업부 # VD사업부 #면접후기
- 지도 자동 구축
- Python
- 성적평균
- Today
- Total
mulll
Euler Tour Tree로 최소 공통 조상(LCA) 구하기 본문
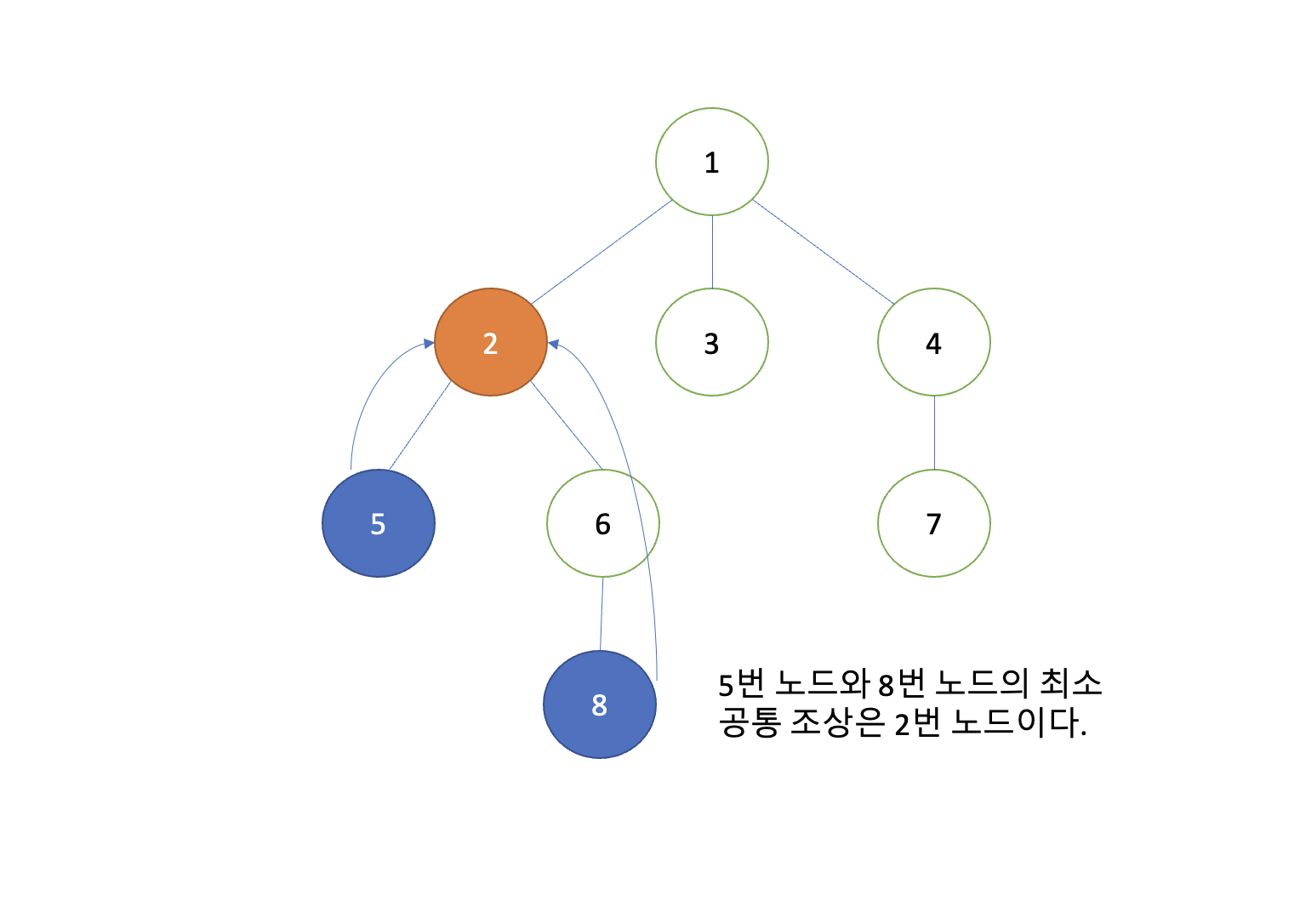
루트 트리에 속한 두 노드의 최소 공통 조상(lowest common ancestor)은 두 노드를 모두 서브트리에 포함하고 있는 가장 낮은 노드 입니다.
이번시간에는 두 노드의 최소공통조상 문제를 Euler Tour Tree로 해결하는 방법을 알아보겠습니다.
먼저, 오일러 투어 트리의 순회 순서는 dfs를 진행하되 dfs가 끝날 때 마다 dfs를 들어가기 전에 노드 번호를 다시 한 번 찍어주는 방식으로 기존의 dfs방식과 유사합니다. 그림으로 먼저 탐색 방식을 확인해보죠.

#include <iostream>
#include <vector>
using namespace std;
vector<int> adj[10];
void dfs(int s, int e){
// s : 현재 노드 번호, e : 이전에 방문 했던 노드 번호
cout << s << ' ';
for(auto u : adj[s]){
if(u != e){
dfs(u, s);
cout << s << ' ';
}
}
}
int main(int argc, const char * argv[]) {
// 각각의 간선의 정보를 인접노드에 양방향으로 넣어줍니다.
// 백준에서 첫번째 노드번호가 부모인지 모를 때는 양방향으로 넣고 dfs돌리는게 효율적이라고 생각합니다.
adj[1].push_back(2);
adj[2].push_back(1);
adj[1].push_back(3);
adj[3].push_back(1);
adj[1].push_back(4);
adj[4].push_back(1);
adj[2].push_back(5);
adj[5].push_back(2);
adj[2].push_back(6);
adj[6].push_back(2);
adj[6].push_back(8);
adj[8].push_back(6);
adj[4].push_back(7);
adj[7].push_back(4);
dfs(1, 0);
return 0;
}
위에 예시로 든 트리의 오일러 투어 경로는 다음과 같은데요. 기본적인 dfs탐색에서 dfs함수가 종료되었을 때 진행했던 노드를 다시 한번 찍어줌으로써 다음과 같이 탐색이 가능합니다.

기존의 dfs로의 출력결과와 차이를 확인해보시기 바랍니다.
오일러투어투리는 트리순회배열을 기반으로 하는데 배열을 만들기 위해, 트리의 깊이를 노드번호와 같이 탐색한 순서대로 배열에 넣어주겠습니다. 그러면 다음과 같은 배열이 만들어질 것입니다. 배열을 만들었긴 하였는데 아직까지는 어떤 용도로 이 배열이 사용될지는 감이잡히지 않네요.

여기서 노드a와 b의 최소 공통 조상을 찾으려면 배열에서 노드a와 b사이의 노드 중 깊이가 최소인 노드를 찾으면 그 노드가 최소 공통 조상이 된다는 것을 알 수 있는데요.

* 노드가 배열에 여러 번 나타날 수 있기 때문에, 노드 a와 b의 위치르 선택하는 방법은 여러 가지가 존재할 수 있습니다. 하지만 어떻게 선택하더라도 최소 공통 조상을 찾을 수 있습니다.
그림으로 다루진 않았지만 8과 7의 노드 사이의 최소공통조상은 배열에서 깊이가 1로 가장 작은 깊이를 갖는 노드 번호 1이 두 노드 사이의 최소 공통조상이 된다는 것을 알 수 있습니다.
거리 계산하기
마지막으로, 노드 a와 b 사이의 거리, 즉, a와 b를 잇는 경로의 길이를 계산하고 싶을 땐, 두 노드의 최소 공통 조상이 존재할 것이고 각각 노드로부터의 거리가 존재할 것인데 두 거리를 합치면 a와 b사이의 거리를 구할 수 있을 것입니다.
depth(n)를 n번 노드의 깊이라고 해보겠습니다.
그러면 노드a와 노드b 사이의 거리는 다음과 같은 일반식을 얻을 수 있습니다.
두 노드 사이의 거리 = depth(a) + depth(b) - 2 * depth(c)
여기서 c는 a와 b의 최소공통조상입니다.
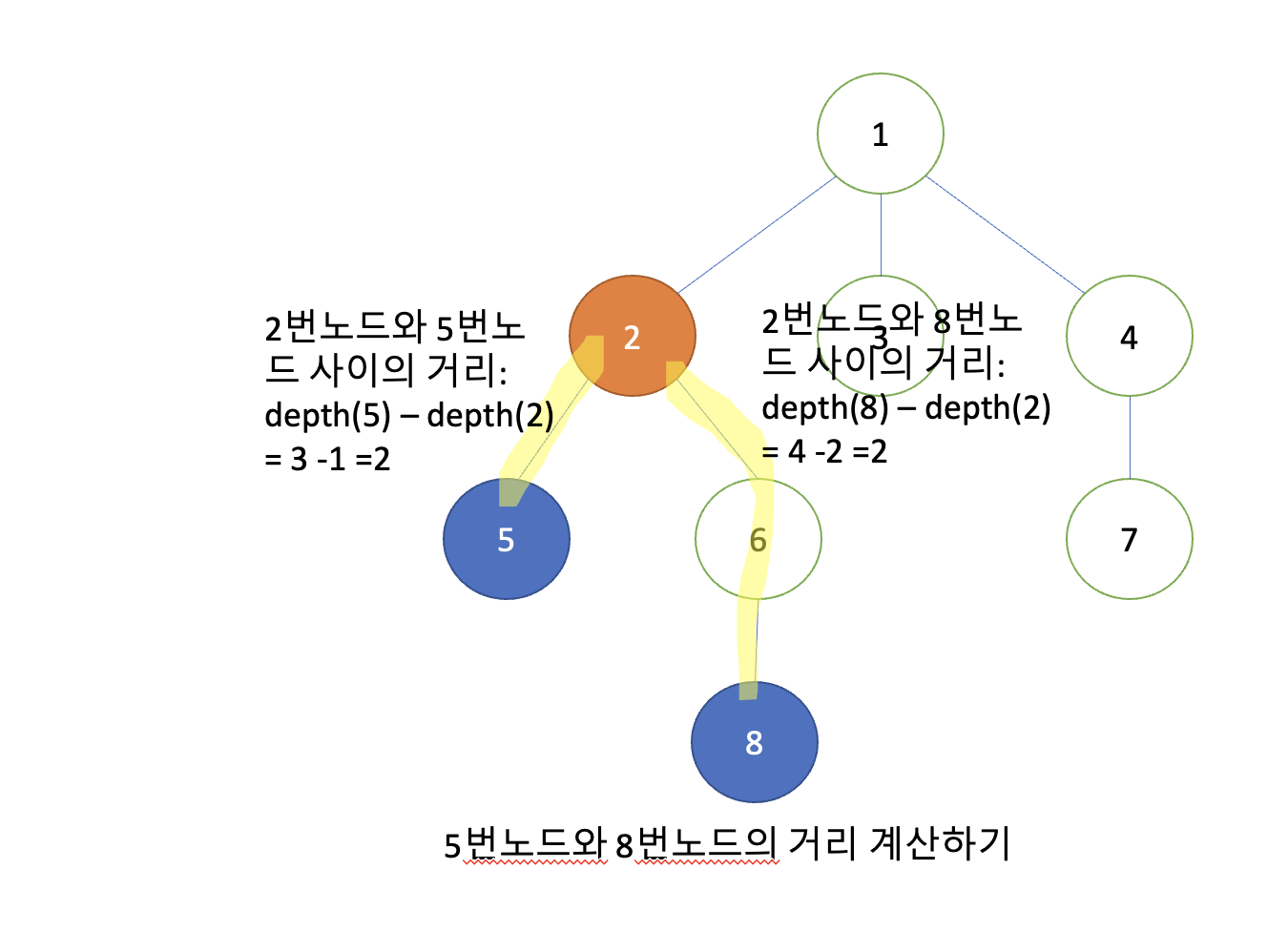
위의 공식에 따라서 5번과 8번 노드 사이의 거리는 3 + 4 - 2 * 2 = 3이 될 수 있음을 알 수 잇습니다.
참고한 자료/서적
알고리즘 트레이닝(인사이트)
같이 풀어보면 좋은 문제들
백준
3584번: 가장 가까운 공통 조상 www.acmicpc.net/problem/3584
11437번: LCA www.acmicpc.net/problem/11437
'algorithm study' 카테고리의 다른 글
| [소프티어] 이미지 프로세싱 / C++ 해설 (0) | 2022.12.03 |
|---|---|
| [소프티어] 마이크로 서버 / C++ 해설 (0) | 2022.12.03 |
| [소프티어] 통근버스 출발 순서 검증하기 / C++ 해설 (0) | 2022.12.02 |
| [소프티어] 슈퍼컴퓨터 클러스터 / C++ 해설 (0) | 2022.11.29 |
| 알고리즘 문제 리뷰를 위주로 포스팅을 합니다. (1) | 2021.05.01 |



